We discovered a new form of vertex colors of graphs (inherited directly form edge-colorings of perfect matchings) in the study of quantum physics questions.
Several new pure graph theoretical questions emerged, and I believe that their answer could lead to exciting insights on the potential of resources of quantum interference.
I have described the question in detail in a youtube video, mathoverflow question, and a contribution to the proceedings of 2nd Croatian Combinatorial Days (arXiv version), and was described in detail by Dustin Mixon.
1) 3.000 Euro Reward
We (Dominik Leitner and me) offer a 3.000 Euro reward for the first solution of our conjecture (either proof or counterexample) (mathoverflow question, Dustin Mixon’s blog, youtube (see Clarification below video), Question1 here):
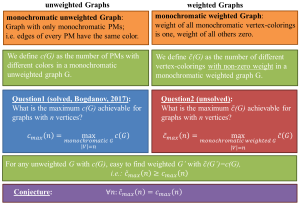
Update January 2021: Not only solutions to Question2, but also counter-examples to the conjecture will be awarded the reward.
The solution has to appear in a respected, peer-reviewed journal (or for counterexamples, there needs to be a way to confirm them, for instance via software). The problem can be concisely formulated in the language of graph theory and combinatorial equation systems.
2) 1.000 Euro Quantum-Graph Best-Paper Award
We (Dominik Leitner and me) offer a 1.000 Euro award for the best paper (Quantum-Graph Best-Paper award) which investigates inherited vertex colors of graphs, derives new results or connections. The next deadline for nominations will be End of April 2024.
- Quantum-Graph Best-Paper Award 2023:
Moshe Y. Vardi, Zhiwei Zhang: Solving Quantum-Inspired Perfect Matching Problems via Tutte’s Theorem-Based Hybrid Boolean Constraints [youtube]
for presenting a fresh perspective in the study of inherited vertex colorings through efficient encodings as Boolean constraint-satisfaction problems using Tutte’s theorem, accompanied by open-source codes enabling convincing numerical experiments.
- Quantum-Graph Best-Paper Award 2022:
L. Sunil Chandran, Rishikesh Gajjala: Perfect Matchings and Quantum Physics: Progress on Krenn’s Conjecture [youtube]
for the confirmation of the conjecture for large classes of simple graphs, as well as the introduction and disproving of a natural generalisation.
Rules: The paper needs to be publically available and correct (peer-reviewed in a respected journal or proceedings, and/or I need to able to understand the results) and the results should be non-trivial/obvious. At the deadline, i will ask for recommendations by experts. In case of two interesting papers, the award could be splitted. Nominations and self-nominations are very welcome.
Known special cases
- [April 2017]: For real, positive weights, it follows from Bogdanov’s lemma that monochromatic weighted graphs cannot exist for (n=4,d>3) and (n>=6,d>2).
- [September 2021]: For monochromatic edges, we proved using SAT solvers that (n=6,d>=3) and (n=8, d>=4) monochromatic weighted graphs don’t exist.
- [February 2022]: For simple graphs with monochromatic edges, a monochromatic graph cannot exist for d>n-2 (even n>=6), due to Chandran & Gajjala.
- [April 2023]: For simple graphs, a monochromatic graph cannot exist for d>n/sqrt(2) (even n>=6), due to Chandran & Gajjala.
- [September 2023]: Unconstraint result (multigraphs with bicolored edges and arbitrary complex weights): For n=4, a monochromatic graph with d>=4 colores does not exist, due to Kevin M. (bafflingbits).
News:
2023.09.04: New special case: For n=4 vertices, it is not possible to create a d=4 colored monochromatic graph, without any conditions (the result works for multi-graphs with bi-colored edges and arbitrary complex weights): github
2023.04.13: New paper by L Sunil Chandran and Rishikesh Gajjala on Perfect matchings and Quantum physics: Bounding the dimension of GHZ states, proving a special case that for simple graphs, a monochromatic graph cannot exist for d>n/sqrt(2).
2023.02.18: Rishikesh Gajjala was awarded the best student poster award in math and computer science at the Prime minister’s research fellowship annual symposium at IIT Madras, for his work on proving a special case of our conjecture, see poster. Congratulations!
2023.01.24: New paper by Moshe Y. Vardi and Zhiwei Zhang (Rice University) on the application of Tutte’s theorem as constraint for encoding the Perfect Matchings under Vertex-Coloring Constraints.
2022.09.26: New paper by Moshe Y. Vardi and Zhiwei Zhang (Rice University) on the computational complexity of Perfect Matchings under Vertex-Color Constraints.
2022.07.04: Bachelor Thesis by Aaron Neugebauer (University of Wuerzburg, Germany) on the conjecture, and a reformulation as color-spanning graphs.
2022.02.11: New paper by L. Sunil Chandran and Rishikesh Gajjala showing that for simple graphs with monochromatic edges, a monochromatic graph cannot exist for d=n-2.
2021.09.27: Using SAT solvers, we proof a few special cases of the conjecture (specifically for graphs with only monochromatic edges).
2021.01.18: Dustin Mixon’s blog post reformulated and generalized the question in a beautiful way.
2020.05.13: New paper on graph-theoretical techniques in artificial intelligence algorithms.
2019.02.23: Mathoverflow question Has this notion of vertex-coloring of graphs been studied? where I explain the concept of bi-chromatic edge-colored graphs and inherited vertex coloring more compactly.
2019.02.16: Questions on the Structure of Perfect Matchings inspired by Quantum Physics – here, together with my colleages Xuemei Gu and Daniel Soltesz, we formalize the ideas of bi-chromatic, edge-colored weighted graph, and the concept of inherited vertex coloring, together with several examples, and a number of noteworthy open question on the topic.
2018.09.24: Mathoverflow question Vertex Coloring inherited from Perfect Matchings (motivated by Quantum Physics) where I explain the idea of inherited vertex coloring and particularily the question for the reward more compactly.
2017.04.12: A post by Ilya Bogdanov, which answeres the question of the reward for the special case of graphs with all weights being real and positive.
Questions and Comments
For any questions and clarifications, please send me an e-Mail.